what type of compound is found when you have a cation attracted to an anion

9.4: Ionic Bonding

1. Final updated

2. Save as PDF

Page ID

38034

Learning Objectives

• To describe the characteristics of ionic bonding.
• To quantitatively describe the energetic factors involved in the formation of an ionic bond.

Ions are atoms or molecules which are electrically charged. Cations are positively charged and anions carry a negative charge. Ions form when atoms gain or lose electrons. Since electrons are negatively charged, an cantlet that loses one or more electrons will become positively charged; an atom that gains one or more electrons becomes negatively charged. Ionic bonding is the attraction between positively- and negatively-charged ions. These oppositely charged ions attract each other to form ionic networks (or lattices). Electrostatics explains why this happens: opposite charges concenter and like charges repel. When many ions concenter each other, they grade large, ordered, crystal lattices in which each ion is surrounded by ions of the contrary charge. More often than not, when metals react with non-metals, electrons are transferred from the metals to the not-metals. The metals grade positively-charged ions and the non-metals form negatively-charged ions.

Generating Ionic Bonds

Ionic bonds form when metals and non-metals chemically react. By definition, a metal is relatively stable if it loses electrons to form a consummate valence trounce and becomes positively charged. Likewise, a not-metal becomes stable by gaining electrons to complete its valence shell and become negatively charged. When metals and not-metals react, the metals lose electrons by transferring them to the non-metals, which gain them. Consequently, ions are formed, which instantly attract each other—ionic bonding.

In the overall ionic compound, positive and negative charges must exist counterbalanced, because electrons cannot be created or destroyed, simply transferred. Thus, the total number of electrons lost by the cationic species must equal the total number of electrons gained by the anionic species.

Example \(\PageIndex{1}\): Sodium Chloride

For example, in the reaction of Na (sodium) and Cl (chlorine), each Cl atom takes one electron from a Na cantlet. Therefore each Na becomes a Na⁺ cation and each Cl atom becomes a Cl^- anion. Due to their opposite charges, they attract each other to grade an ionic lattice. The formula (ratio of positive to negative ions) in the lattice is \(\ce{NaCl}\).

\[\ce{2Na (s) + Cl 2(chiliad) \rightarrow 2NaCl (s)} \nonumber\]

These ions are arranged in solid NaCl in a regular iii-dimensional arrangement (or lattice):

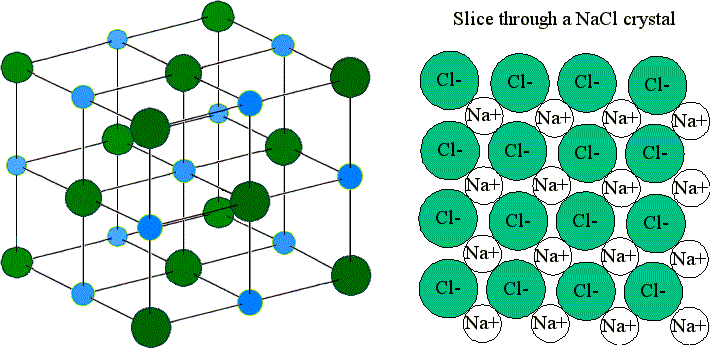
NaCl lattice. (left) iii-D structure and (right) elementary 2D slice through lattes. Images used with permission from Wikipedia and Mike Blaber.

The chlorine has a high analogousness for electrons, and the sodium has a low ionization energy. Thus the chlorine gains an electron from the sodium cantlet. This tin can exist represented using ewis dot symbols (here we will consider ane chlorine atom, rather than Cl_two):

The arrow indicates the transfer of the electron from sodium to chlorine to class the Na⁺ metallic ion and the Cl^- chloride ion. Each ion now has an octet of electrons in its valence shell:

• Na^+: 2s²2p^{half dozen}
• Cl^-: 3s^two3p^{half dozen}

Energetics of Ionic Bond Formation

Ionic bonds are formed when positively and negatively charged ions are held together by electrostatic forces. Consider a single pair of ions, one cation and one anion. How strong volition the strength of their allure be? According to Coulomb'due south Law, the free energy of the electrostatic attraction (\(E\)) between two charged particles is proportional to the magnitude of the charges and inversely proportional to the internuclear distance between the particles (\(r\)):

\[E \propto \dfrac{Q_{i}Q_{two}}{r} \label{Eq1a} \]

\[ East = k\dfrac{Q_{ane}Q_{ii}}{r} \characterization{Eq1b} \]

where each ion's accuse is represented by the symbol Q. The proportionality constant thousand is equal to ii.31 × 10⁻²⁸ J·m. This value of k includes the charge of a single electron (1.6022 × 10^−xix C) for each ion. The equation can also be written using the charge of each ion, expressed in coulombs (C), incorporated in the constant. In this instance, the proportionality constant, k, equals 8.999 × 109 J·g/C². In the instance given, Q ₁ = +1(1.6022 × 10⁻¹⁹ C) and Q ₂ = −1(1.6022 × 10⁻¹⁹ C). If Q _ane and Q _ii accept opposite signs (as in NaCl, for example, where Q _i is +i for Na⁺ and Q _two is −1 for Cl⁻), then E is negative, which means that energy is released when oppositely charged ions are brought together from an infinite distance to class an isolated ion pair.

Energy is always released when a bond is formed and correspondingly, it e'er requires energy to break a bond.

As shown by the green curve in the lower one-half of Effigy \(\PageIndex{1}\), the maximum energy would exist released when the ions are infinitely shut to each other, at r = 0. Considering ions occupy space and take a construction with the positive nucleus being surrounded by electrons, however, they cannot be infinitely close together. At very short distances, repulsive electron–electron interactions between electrons on adjacent ions become stronger than the attractive interactions between ions with opposite charges, as shown by the red bend in the upper one-half of Figure \(\PageIndex{1}\). The total energy of the system is a balance between the attractive and repulsive interactions. The purple bend in Figure \(\PageIndex{i}\) shows that the total energy of the system reaches a minimum at r ₀, the point where the electrostatic repulsions and attractions are exactly balanced. This distance is the aforementioned as the experimentally measured bail distance.

Figure \(\PageIndex{i}\): A Plot of Potential Energy versus Internuclear Distance for the Interaction between a Gaseous Na⁺ Ion and a Gaseous Cl⁻ Ion. The energy of the system reaches a minimum at a particular distance (r ₀) when the attractive and repulsive interactions are balanced.

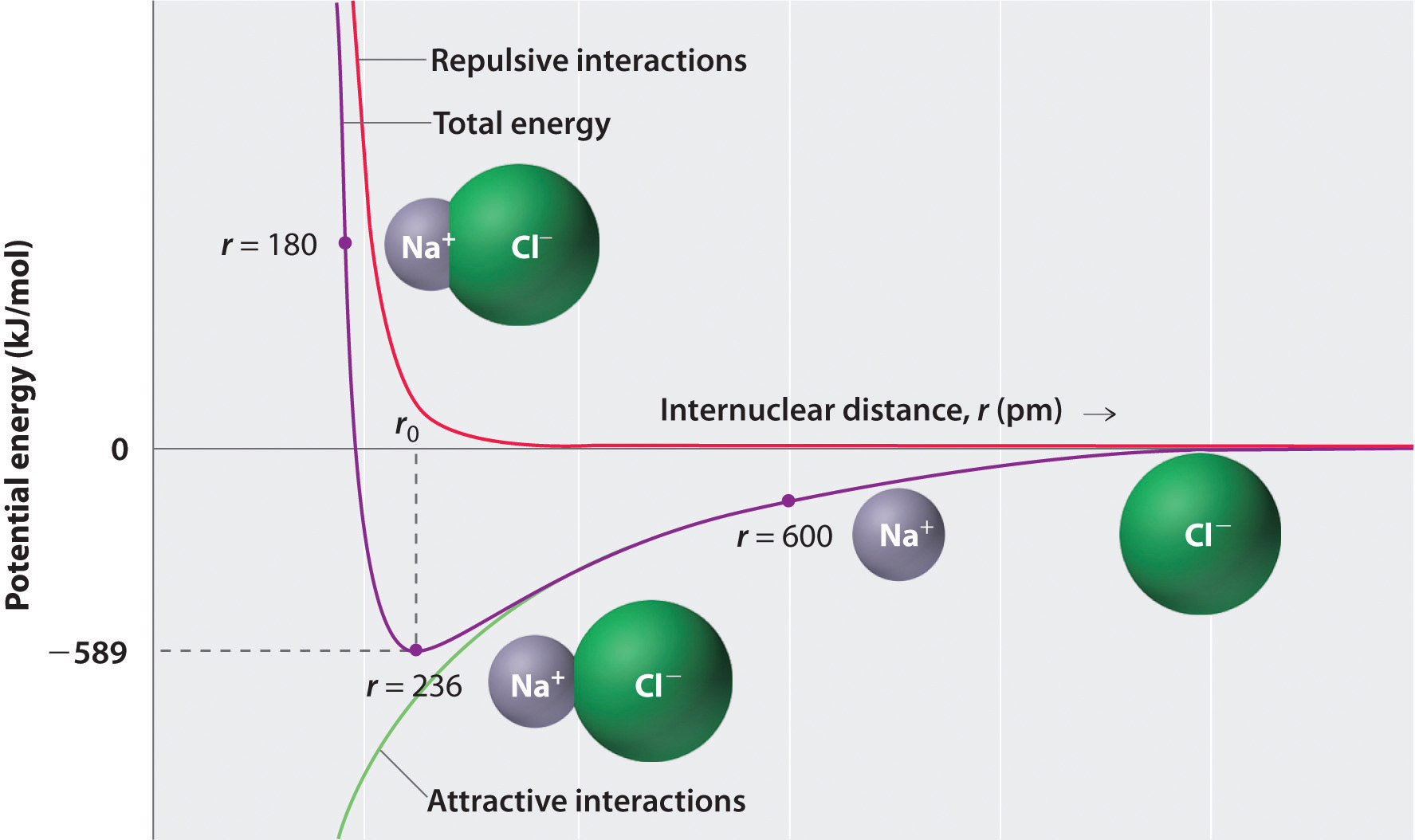
Consider the free energy released when a gaseous \(Na^+\) ion and a gaseous \(Cl^-\) ion are brought together from r = ∞ to r = r ₀. Given that the observed gas-stage internuclear distance is 236 pm, the energy change associated with the formation of an ion pair from an \(Na^+_{(grand)}\) ion and a \(Cl^-_{(g)}\) ion is every bit follows:

\[ \begin{align*} E &= k\dfrac{Q_{1}Q_{2}}{r_{0}} \\[4pt] &= (two.31 \times {ten^{ - 28}}\rm{J}\cdot \cancel{m} ) \left( \dfrac{( + ane)( - 1)}{236\; \cancel{pm} \times 10^{ - 12} \cancel{thousand/pm}} \right) \\[4pt] &= - ix.79 \times x^{ - xix}\; J/ion\; pair \characterization{Eq2} \finish{align*}\]

The negative value indicates that energy is released. Our convention is that if a chemic process provides energy to the exterior earth, the free energy change is negative. If information technology requires energy, the energy alter is positive. To calculate the free energy change in the formation of a mole of NaCl pairs, we need to multiply the energy per ion pair by Avogadro's number:

\[ East=\left ( -9.79 \times 10^{ - xix}\; J/ \cancel{ion pair} \right )\left ( half-dozen.022 \times ten^{ 23}\; \cancel{ion\; pair}/mol\correct )=-589\; kJ/mol \characterization{Eq3} \]

This is the free energy released when 1 mol of gaseous ion pairs is formed, not when 1 mol of positive and negative ions condenses to form a crystalline lattice. Because of long-range interactions in the lattice construction, this free energy does non stand for directly to the lattice energy of the crystalline solid. Yet, the big negative value indicates that bringing positive and negative ions together is energetically very favorable, whether an ion pair or a crystalline lattice is formed.

We summarize the of import points about ionic bonding:

• At r ₀, the ions are more than stable (have a lower potential energy) than they are at an infinite internuclear distance. When oppositely charged ions are brought together from r = ∞ to r = r ₀, the energy of the organization is lowered (energy is released).
• Because of the low potential free energy at r ₀, energy must be added to the system to separate the ions. The corporeality of free energy needed is the bond energy.
• The energy of the system reaches a minimum at a particular internuclear altitude (the bond distance).

Case \(\PageIndex{ii}\): LiF

Calculate the amount of energy released when i mol of gaseous Li⁺F⁻ ion pairs is formed from the separated ions. The observed internuclear distance in the gas stage is 156 pm.

Given: cation and anion, amount, and internuclear distance

Asked for: energy released from formation of gaseous ion pairs

Strategy:

Substitute the advisable values into Equation \(\ref{Eq1b}\) to obtain the energy released in the formation of a single ion pair and then multiply this value past Avogadro's number to obtain the energy released per mole.

Solution:

Inserting the values for Li⁺F⁻ into Equation \(\ref{Eq1b}\) (where Q ₁ = +ane, Q ₂ = −i, and r = 156 pm), nosotros find that the energy associated with the formation of a unmarried pair of Li⁺F⁻ ions is

\[ \brainstorm{align*} E &=k \dfrac{Q_1Q_2}{r_0} \\[4pt] &=\left(2.31 \times 10^{−28} J⋅\abolish{grand} \right) \left(\dfrac{\text{(+ane)(−1)}}{156\; pm \times x^{−12} \cancel{one thousand/pm}} \right)\\[4pt] &=−1.48 \times x^{−18} \finish{align*}\]

Then the free energy released per mole of Li⁺F⁻ ion pairs is

\[ \begin{marshal*} E&= \left(−1.48 \times 10^{−18} J/ \cancel{\text{ion pair}}\right) \left(vi.022 \times 10^{23} \cancel{\text{ion pair}}/mol\right)\\[4pt] &−891 \;kJ/mol \stop{marshal*}\]

Considering Li⁺ and F⁻ are smaller than Na⁺ and Cl⁻ (see Section 7.three), the internuclear distance in LiF is shorter than in NaCl. Consequently, in accordance with Equation \(\ref{Eq1b}\), much more energy is released when i mol of gaseous Li⁺F⁻ ion pairs is formed (−891 kJ/mol) than when ane mol of gaseous Na⁺Cl⁻ ion pairs is formed (−589 kJ/mol).

Do \(\PageIndex{2}\): Magnesium oxide

Summate the corporeality of energy released when 1 mol of gaseous \(\ce{MgO}\) ion pairs is formed from the separated ions. The internuclear altitude in the gas phase is 175 pm.

Answer

−3180 kJ/mol = −3.eighteen × 10³ kJ/mol

Electron Configuration of Ions

How does the free energy released in lattice formation compare to the energy required to strip abroad a 2d electron from the Na⁺ ion? Since the Na⁺ ion has a element of group 0 electron configuration, stripping away the adjacent electron from this stable arrangement would require more energy than what is released during lattice formation (Sodium I₂ = four,560 kJ/mol). Thus, sodium is present in ionic compounds as Na⁺ and not Na^two+. Likewise, adding an electron to fill a valence trounce (and accomplish noble gas electron configuration) is exothermic or only slightly endothermic. To add an additional electron into a new subshell requires tremendous energy - more than the lattice energy. Thus, we find Cl^- in ionic compounds, but not Cl^2-.

Table \(\PageIndex{1}\): Lattice energies range from around 700 kJ/mol to 4000 kJ/mol:

Compound	Lattice Energy (kJ/mol)
LiF	1024
LiI	744
NaF	911
NaCl	788
NaI	693
KF	815
KBr	682
KI	641
MgFtwo	2910
SrClii	2130
MgO	3938

This amount of energy can recoup for values as large as I_iii for valence electrons (i.e. can strip away up to three valence electrons). Considering well-nigh transition metals would require the removal of more than three electrons to accomplish a noble gas core, they are not found in ionic compounds with a noble gas cadre. A transition metal e'er loses electrons first from the college 's' subshell, before losing from the underlying 'd' subshell. (The remaining electrons in the unfilled d subshell are the reason for the brilliant colors observed in many transition metal compounds!) For instance, fe ions will not form a noble gas core:

• Atomic number 26: [Ar]4s²3d⁶
• Fe^two+: [Ar] 3d⁶
• Fe³⁺: [Ar] 3d⁵

Some metallic ions tin can form a pseudo noble gas cadre (and be colorless), for example:

• Ag: [Kr]5s^ane4d^x Ag⁺ [Kr]4d¹⁰ Compound: AgCl
• Cd: [Kr]5sⁱⁱ4d^ten Cd^two+ [Kr]4d¹⁰ Compound: CdS

The valence electrons practice not adhere to the "octet rule" in this case (a limitation of the usefulness of this rule). Note: The silvery and cadmium atoms lost the 5s electrons in achieving the ionic country.

When a positive ion is formed from an atom, electrons are always lost showtime from the subshell with the largest principle quantum number

Polyatomic Ions

Non all ionic compounds are formed from only two elements. Many polyatomic ions exist, in which two or more atoms are bound together by covalent bonds. They form a stable grouping which carries a charge (positive or negative). The group of atoms as a whole acts as a charged species in forming an ionic chemical compound with an oppositely charged ion. Polyatomic ions may be either positive or negative, for example:

• NH₄ ⁺ (ammonium) = cation
• So₄ ^two- (sulfate) = anion

The principles of ionic bonding with polyatomic ions are the same as those with monatomic ions. Oppositely charged ions come together to form a crystalline lattice, releasing a lattice energy. Based on the shapes and charges of the polyatomic ions, these compounds may form crystalline lattices with interesting and complex structures.

Summary

The amount of energy needed to separate a gaseous ion pair is its bond energy. The formation of ionic compounds are usually extremely exothermic . The strength of the electrostatic attraction between ions with opposite charges is directly proportional to the magnitude of the charges on the ions and inversely proportional to the internuclear distance. The total free energy of the system is a balance between the repulsive interactions between electrons on adjacent ions and the bonny interactions between ions with reverse charges.

nevilleaple1962.blogspot.com

Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map:_A_Molecular_Approach_%28Tro%29/09:_Chemical_Bonding_I-_Lewis_Structures_and_Determining_Molecular_Shapes/9.04:_Ionic_Bonding

Share this post